Комплексно-сопряженные числа
Определение
Комплексно сопряженные числа представляют собой пару комплексных чисел, которые имеют одинаковые действительные части и равные по модулю, но противоположные по знаку мнимые части.
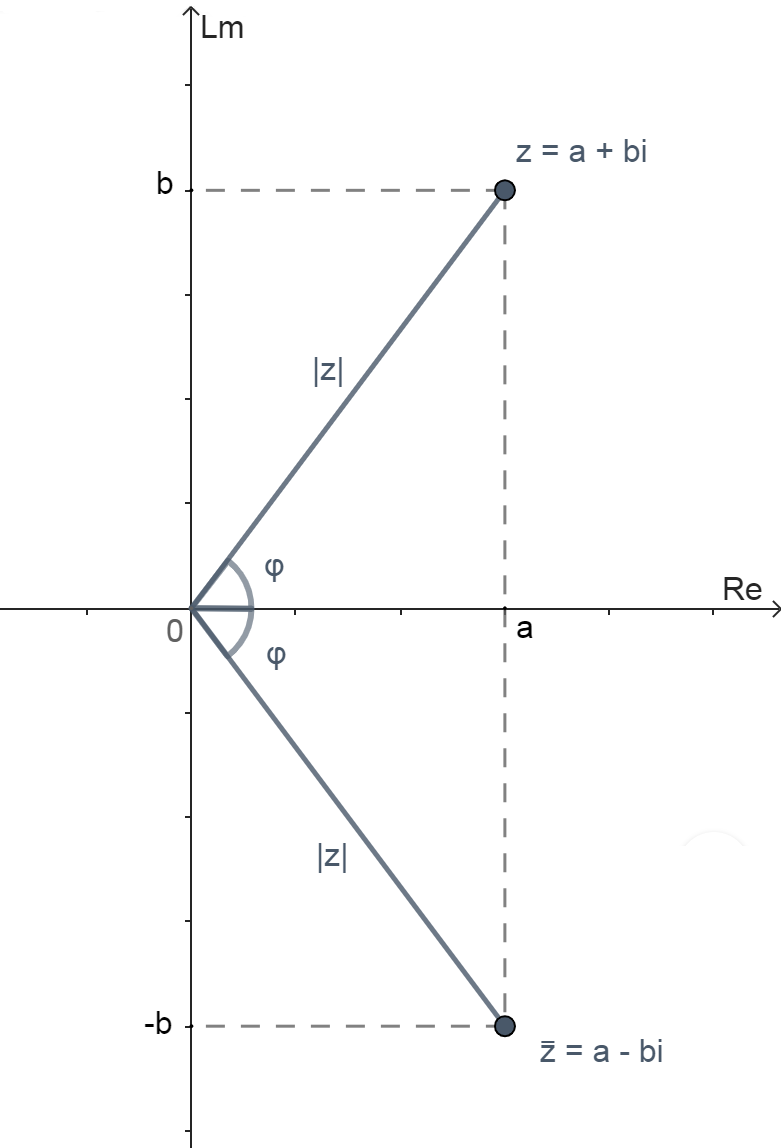Геометрическое представление числа $$z$$ и его сопряжённого числа $$\overline{z}$$ на комплексной плоскости
$$z = a + bi$$
$$z\text{ - комплексное число}$$
$$a,b\text{ - вещественные числа}$$
$$i\text{ - мнимая единица}$$
$$\overline{z} = a - bi$$
$$\overline{z}\text{ - число сопряженное числу} z$$
Число, сопряжённое к числу $$z$$, обозначается $$\overline{z}$$.
Например, числа $$3+7i$$ и $$3-7i$$ являются сопряженными.
Если комплексное число представлено в тригонометрической форме $$z = \lvert z \rvert(cos(φ) + i sin(φ))$$, где $$\lvert z \rvert\text{ - модуль комплексного числа}$$, $$φ \text{ - аргумент комплексного числа}$$, $$cos, sin\text{ - косинус и синус}$$ и $$i\text{ - мнимая единица}$$ то сопряженное число для данного комплексного числа запишется как $$\overline{z} = \lvert z \rvert(cos(φ) - i sin(φ))$$.
Например, числа $$3 \cdot \left(\cos{\dfrac{\pi}{2}} + i \sin{\dfrac{\pi}{2}}\right)$$ и $$3 \cdot \left(\cos{\dfrac{\pi}{2}} - i \sin{\dfrac{\pi}{2}}\right)$$ являются сопряженными.
Если комплексное число представлено в показательной форме $$z = \lvert z \rvert \cdot e^{iφ}$$, где $$\lvert z \rvert\text{ - модуль комплексного числа}$$, $$φ \text{ - аргумент комплексного числа}$$, $$e \text{ - число Эйлера}$$ и $$i\text{ - мнимая единица}$$ то сопряженное число для данного комплексного числа запишется как $$\overline{z} = \lvert z \rvert \cdot e^{-iφ}$$.
Например, числа $$2 \cdot e^{i \, \cdot \, \left(\dfrac{\pi}{3}\right)}$$ и $$2 \cdot e^{-i \, \cdot \,\left(\dfrac{\pi}{3}\right)}$$ являются сопряженными.