Формы представления комплексного числа
Определение
Комплексное число можно представить тремя разными формами, а именно в алгебраической, тригонометрической и показательной. Выбор формы зависит от того какие арифметические операции с комплексными числами необходимо выполнить.
Алгебраическая форма
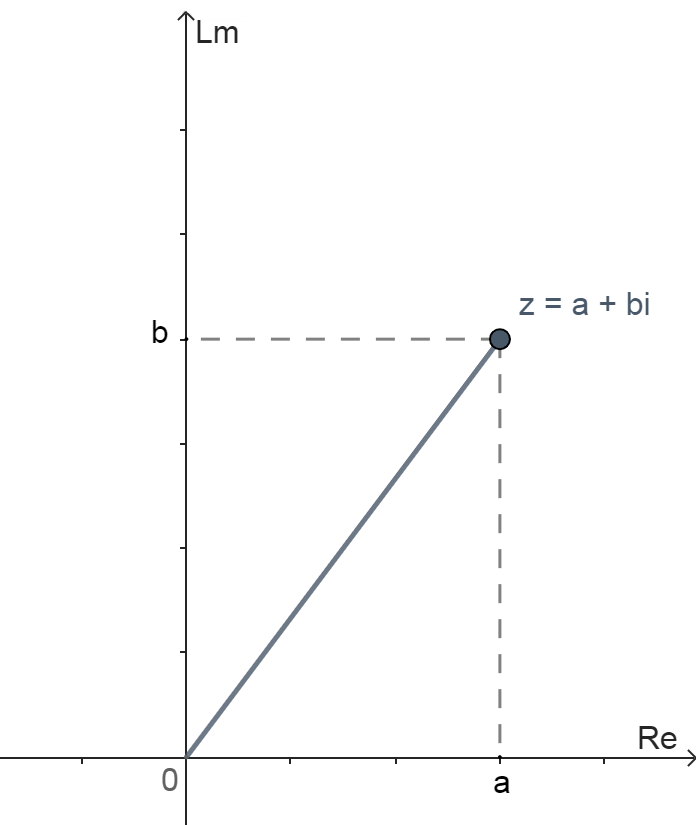Геометрическое представление комплексного числа $$z$$ в алгебраической форме на комплексной плоскости
$$z = a + bi$$
$$z\text{ - комплексное число}$$
$$a,b\text{ - вещественные числа}$$
$$i\text{ - мнимая единица}$$
Алгебраическую форму записи комплексного числа $$z = a + bi$$ используют для более удобного выполнения алгебраических операций с комплексными числами, таких как сложение, вычитание, умножение и деление.
Приведем примеры комплексных чисел записанных в алгебраической форме: $$2 + 3i$$, $$2 - 3i$$, $$-5 + 7i$$, $$-1 - 2i$$, $$8i$$, $$-4i$$ и т.д.
Тригонометрическая форма
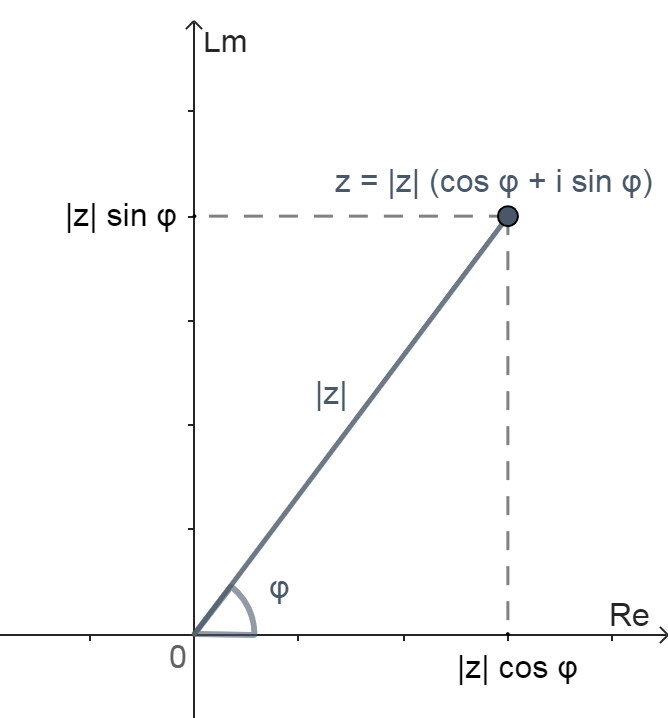Геометрическое представление комплексного числа $$z$$ в тригонометрической форме на комплексной плоскости
$$z = \lvert z \rvert(cos(φ) + i sin(φ))$$
$$z\text{ - комплексное число}$$
$$\lvert z \rvert\text{ - модуль комплексного числа}$$
$$φ \text{ - аргумент комплексного числа}$$
$$cos, sin\text{ - косинус и синус}$$
$$i\text{ - мнимая единица}$$
В тригонометрической форме $$z = \lvert z \rvert(cos(φ) + i sin(φ))$$ значительно упрощаются операции умножения, деления и возведения в степень. Также при использовании тригонометрической формы возможно извлечение корня.
Чтобы представить комплексное число в тригонометрической форме необходимо вычислить модуль $$\lvert z \rvert$$ и аргумент $$arg(z)$$, который представляет собой угол $$φ$$ между радиус-вектором соответствующей точки и положительной вещественной полуосью.
Приведем примеры комплексных чисел записанных в тригонометрической форме: $$2 \cdot \left(\cos{\dfrac{\pi}{3} } + i \cdot \sin{\dfrac{\pi}{3} }\right)$$, $$\sqrt{12} \cdot \left(\cos{\frac{\pi}{6} } + i \cdot \sin{\frac{\pi}{6} }\right)$$ и т.д.
Показательная форма
$$z = \lvert z \rvert \cdot e^{iφ}$$
$$z\text{ - комплексное число}$$
$$\lvert z \rvert\text{ - модуль комплексного числа}$$
$$φ \text{ - аргумент комплексного числа}$$
$$e \text{ - число Эйлера}$$
$$i\text{ - мнимая единица}$$
В показательной форме $$z = \lvert z \rvert \cdot e^{iφ}$$ удобно проводить операции умножения и деления комплексных чисел. Показательная форма комплексного числа используется в различных областях математики и физики. В теории цепей комплексные числа и их показательная форма применяются для анализа переменного тока, особенно в контексте синусоидальных сигналов. Показательная форма упрощает работу с периодическими функциями и их разложением в ряд Фурье. В квантовой механики комплексные числа и их представление в показательной форме используются для описания волновых функций и вероятностных амплитуд.
Показательная форма тесно связана с тригонометрическими функциями через формулу Эйлера $$e^{iφ} = cos(φ) + isin(φ)$$, что позволяет удобно переходить между различными формами представления.