Уведомление

Мы и выбранные партнеры используем файлы «cookie» или аналогичные технологии, указанные в политике в отношении файлов «cookie».
Вы можете дать согласие на использование таких технологий, прокручивая эту страницу, используя любую ссылку или кнопку за пределами этого уведомления или продолжая просматривать материалы иным способом.
Дополнительно о категориях собираемой личной информации и целях, в которых такая информация будет использоваться, см. в наших правилах обеспечения конфиденциальности персональных данных.
Продолжая пользоваться сайтом, вы соглашаетесь с использованием файлов cookie.

Калькулятор гиперболического секанса

Калькулятор вычислит значение гиперболического секанса sch(x) и представит пошаговое решение. В случае, если значение аргумента x задано в градусах, то будет выполнен перевод из градусов в радианы.

Примеры ввода ▽
Дроби 3/7 или -3/7
Квадратный корень sqrt(3) sqrt(4.5) sqrt(1/2)
Степень 4^2 или (1/2)^2
Скобки (1/2)/4
Число π записывается как pi, например, 2pi, pi/2, 3pi/2, sqrt(pi/3)
$$sch(x) = \dfrac{2}{{e}^{x} + {e}^{-x}}$$
$$(x) = $$
Ответ$$sch\left(\dfrac{7}{36}\pi\right) = $$$$0.838607671053286$$Решение$$sch\left(\dfrac{7}{36}\pi\right) = \dfrac{2}{{e}^{\left(\dfrac{7}{36}\pi\right)} + {e}^{-\left(\dfrac{7}{36}\pi\right)}} = $$$$\dfrac{2}{{e}^{-\dfrac{7}{36}\pi} + {e}^{\dfrac{7}{36}\pi}}=0.838607671053286$$

Гиперболический секанс

Определение Гиперболический секанс, обозначаемый как $$sch(x)$$ или $$sech(x)$$, является одной из гиперболических функций. Он определяется как отношение 2 к сумме экспоненты и ее обратного значения: $$sch(x) = \dfrac{2}{{e}^{x} + {e}^{-x}}$$, где $$e$$ - число Эйлера, приближенное значение которого равно примерно $$2.71828$$.

В функции гиперболического секанса $$sch(x)$$, переменная $$x$$ представляет собой аргумент функции, то есть значение, для которого мы вычисляем гиперболический секанс. Значение $$x$$ может быть любым действительны или комплексным числом.

Eсли $$x$$ интерпретируется как угол, то обычно предполагается, что угол задан в радианах. Гиперболический секанс может быть использован для вычисления значений функций, связанных с геометрией и физикой, где углы обычно измеряются в радианах. Однако, если угол задан в градусах, его необходимо преобразовать в радианы.

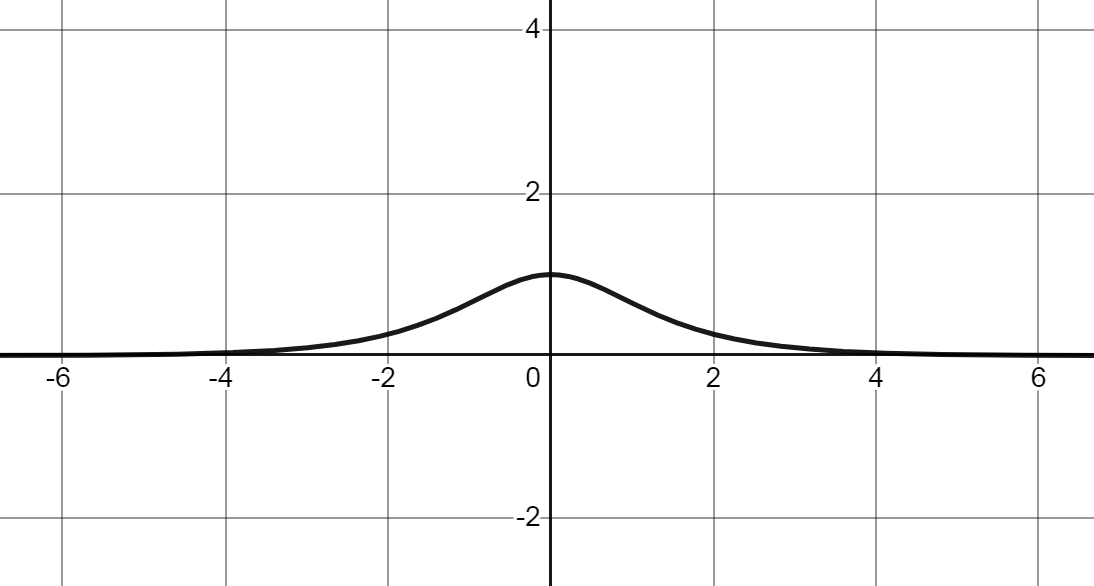График гиперболического секанса
График $$sch(x)$$

Гиперболический секанс можно выразить через функцию секанса с использованием мнимого аргумента: $$sch(x) = \frac{1}{cos(ix)}$$

Другие калькуляторы
Химия Таблицы Таблица химических элементов Элементы I группы таблицы Менделеева Элементы II группы таблицы Менделеева Элементы III группы таблицы Менделеева Элементы IV группы таблицы Менделеева Элементы V группы таблицы Менделеева Элементы VI группы таблицы Менделеева Элементы VII группы таблицы Менделеева Элементы VIII группы таблицы Менделеева Элементы 1 периода таблицы Менделеева Элементы 2 периода таблицы Менделеева Элементы 3 периода таблицы Менделеева Элементы 4 периода таблицы Менделеева Элементы 5 периода таблицы Менделеева Элементы 6 периода таблицы Менделеева Элементы 7 периода таблицы Менделеева Таблица номеров CAS химических элементов Калькуляторы Калькулятор валентности Калькулятор массы вещества Калькулятор абсолютной молекулярной массы Калькулятор относительной молекулярной массы Калькулятор молярной массы Калькулятор массовой доли элемента в веществе Калькулятор количества вещества Калькулятор объема газа Калькулятор молярного объема газа Электронные конфигурации и графические схемы атомов
Астрономия Таблицы Таблица первой, второй и третей космических скоростей планет Солнечной системы Калькуляторы Калькулятор ускорения свободного падения Калькулятор расстояния до видимого горизонта Калькулятор космической скорости Калькулятор солнечных масс Калькулятор земных масс
Информатика Калькулятор двоичных чисел Калькулятор преобразования экспоненциальной записи
Математика Арифметика Калькулятор дробей Калькулятор преобразования дроби Калькулятор расчета процентов Алгебра Калькулятор алгебраических выражений Калькулятор сравнения математических выражений Калькулятор классов вычетов по модулю Линейная алгебра Калькулятор длины отрезка Калькулятор середины отрезка Тригонометрия Калькулятор гиперболического синуса Калькулятор гиперболического косинуса Калькулятор гиперболического тангенса Калькулятор гиперболического котангенса Калькулятор гиперболического секанса Калькулятор гиперболического косеканса Комплексные числа Калькулятор действий над комплексными числами Калькулятор формы представления комплексного числа Калькулятор модуля комплексного числа Калькулятор аргумента комплексного числа Калькулятор возведения в степень комплексного числа Калькулятор корня из комплексного числа Калькулятор комплексно-сопряженного числа Калькулятор обратной величины комплексного числа
Геометрия Куб Калькулятор длины ребра куба Калькулятор диагонали куба Калькулятор диагонали куба по радиусу вписанной сферы Калькулятор диагонали куба по радиусу описанной сферы Калькулятор диагонали куба по площади его поверхности Калькулятор диагонали куба по его объему Калькулятор радиуса вписанной сферы в куб Калькулятор радиуса вписанной сферы в куб по длине его диагонали Калькулятор радиуса вписанной сферы в куб по радиусу описанной сферы Калькулятор радиуса вписанной сферы в куб по площади его поверхности Калькулятор радиуса вписанной сферы в куб по его объему Калькулятор радиуса описанной сферы около куба Калькулятор радиуса описанной сферы около куба по длине его диагонали Калькулятор радиуса описанной сферы около куба по радиусу вписанной сферы Калькулятор радиуса описанной сферы около куба по площади его поверхности Калькулятор радиуса описанной сферы около куба по его объему Калькулятор площади поверхности куба Калькулятор площади поверхности куба по длине его диагонали Калькулятор площади поверхности куба по радиусу вписанной сферы Калькулятор площади поверхности куба по радиусу описанной сферы Калькулятор площади поверхности куба по его объему Калькулятор объема куба Калькулятор объема куба по его диагонали Калькулятор объема куба по радиусу вписанной сферы Калькулятор объема куба по радиусу описанной сферы Калькулятор объема куба по его площади поверхности Прямоугольный параллелепипед Калькулятор длины ребра прямоугольного параллелепипеда Калькулятор диагонали прямоугольного параллелепипеда Калькулятор площади поверхности прямоугольного параллелепипеда Калькулятор объема прямоугольного параллелепипеда Призма Число граней, вершин и ребер у призмы Калькулятор высоты призмы Калькулятор периметра перпендикулярного сечения произвольной призмы Калькулятор длины бокового ребра произвольной призмы Калькулятор площади боковой поверхности прямой призмы Калькулятор площади боковой поверхности произвольной призмы Калькулятор площади основания призмы Калькулятор площади поверхности призмы Калькулятор объема призмы Пирамида Число граней, вершин и ребер у пирамиды Калькулятор высоты пирамиды Калькулятор апофемы пирамиды Калькулятор периметра основания пирамиды Калькулятор площади боковой поверхности пирамиды Калькулятор площади основания пирамиды Калькулятор площади поверхности пирамиды Калькулятор объема пирамиды Тетраэдр Калькулятор длины ребра правильного тетраэдра Калькулятор высоты правильного тетраэдра Калькулятор высоты тетраэдра по радиусу вписанной сферы Калькулятор высоты тетраэдра по радиусу описанной сферы Калькулятор высоты тетраэдра по площади его поверхности Калькулятор высоты тетраэдра по его объему Калькулятор радиуса вписанной сферы в правильный тетраэдр Калькулятор радиуса вписанной сферы в тетраэдр по его высоте Калькулятор радиуса вписанной сферы в тетраэдр по радиусу описанной сферы Калькулятор радиуса вписанной сферы в тетраэдр по площади его поверхности Калькулятор радиуса вписанной сферы в тетраэдр по его объему Калькулятор радиуса описанной сферы около правильного тетраэдра Калькулятор радиуса описанной сферы около тетраэдра по его высоте Калькулятор радиуса описанной сферы около тетраэдра по радиусу вписанной сферы Калькулятор радиуса описанной сферы около тетраэдра по площади его поверхности Калькулятор радиуса описанной сферы около тетраэдра по его объему Калькулятор площади поверхности правильного тетраэдра Калькулятор площади поверхности тетраэдра по его высоте Калькулятор площади поверхности тетраэдра по радиусу вписанной сферы Калькулятор площади поверхности тетраэдра по радиусу описанной сферы Калькулятор площади поверхности тетраэдра по его объему Калькулятор объема произвольного тетраэдра Калькулятор объема правильного тетраэдра Калькулятор объема тетраэдра по его высоте Калькулятор объема тетраэдра по радиусу вписанной сферы Калькулятор объема тетраэдра по радиусу описанной сферы Калькулятор объема тетраэдра по площади его поверхности Шар Калькулятор радиуса шара Калькулятор диаметра шара Калькулятор площади поверхности шара Калькулятор объема шара Круговой цилиндр Калькулятор радиуса основания кругового цилиндра Калькулятор диаметра основания кругового цилиндра Калькулятор высоты кругового цилиндра Калькулятор площади поверхности кругового цилиндра Калькулятор объема кругового цилиндра Конус Калькулятор радиуса основания конуса Калькулятор высоты конуса Калькулятор площади боковой поверхности конуса Калькулятор площади основания конуса Калькулятор площади поверхности конуса Калькулятор объема конуса Эллипсоид Калькулятор объёма эллипсоида
Физика Калькулятор механической работы Калькулятор механической мощности
Конвертеры Конвертер единиц измерения СИ Конвертер объема Перевод градусов, минут и секунд в радианы Конвертеры старорусских мер длины Конвертер саженей Конвертер верст Конвертер аршин Конвертер пядей Конвертер вершков
© 2024 d-calc.ru
Все права защищены.
Копирование материалов сайта запрещено.
Обратная связь
support@d-calc.ru
Правила использования «cookie»
Политика конфиденциальности
Уведомление
Cookie