Аргумент комплексного числа
Определение
Аргумент комплексного числа $$z$$ представляет собой угол $$φ$$ между радиус-вектором соответствующей точки и положительной вещественной полуосью.
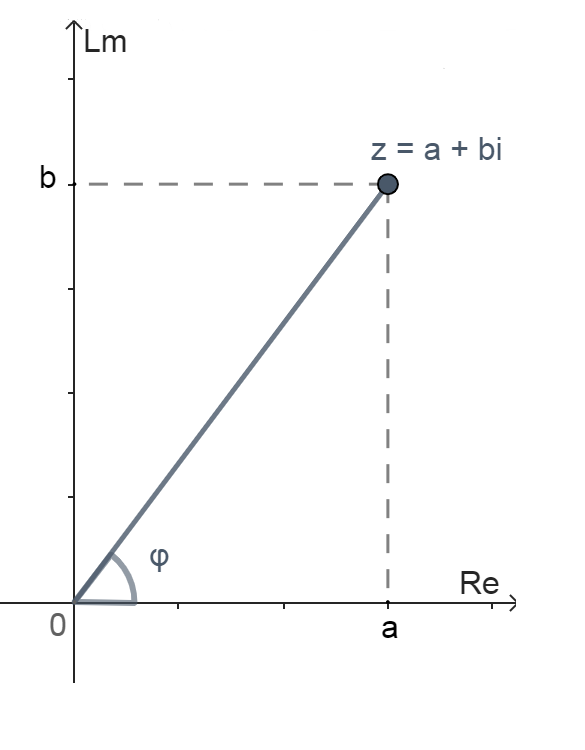Геометрическое представление аргумента комплексного числа
$$z = a + bi$$
$$z\text{ - комплексное число}$$
$$a,b\text{ - вещественные числа}$$
$$i\text{ - мнимая единица}$$
$$Arg(z) = ∠φ\text{ - аргумент комплексного числа}$$
Как видно, любое не нулевое комплексное число имеет бесконечное число значений аргумента, которые отличаются на $$2\pi k$$, то есть на целое число полных оборотов, где $$к$$ – целое число.
Величина угла $$φ$$ зависит от значений вещественных чисел $$a$$ и $$b$$. Если $$a > 0$$ то $$Arg(z) = arctg\left(\frac{b}{a}\right)$$, если $$a < 0$$ то угол увеличивается на $$\pi$$ радиан $$Arg(z) = arctg\left(\frac{b}{a}\right) + \pi$$. Если $$b > 0 \text{ и } a = 0$$ $$Arg(z) = \frac{\pi}{2}$$, иначе $$Arg(z) = -\frac{\pi}{2}$$ если $$b < 0 \text{ и } a = 0$$. Где arctg - Арктангенс.
Значение аргумента не определено, если комплексное число равно нулю.
Главное значение аргумента комплексного числа
Главное значение аргумента $$arg(z)$$ характерно тем, что оно должно быть больше −180 градусов и меньше, либо равно 180 градусам.
Для главного значения аргумента справедливы соотношения:
$$arg(z) = arctg\left(\frac{b}{a}\right), a > 0$$
$$arg(z) = arctg\left(\frac{b}{a}\right) + \pi, a < 0 \text{ и } b ≥ 0$$
$$arg(z) = arctg\left(\frac{b}{a}\right) - \pi, a < 0 \text{ и } b < 0$$
$$arg(z) = \frac{\pi}{2}, b > 0 \text{ и } a = 0$$
$$arg(z) = -\frac{\pi}{2}, b < 0 \text{ и } a = 0$$